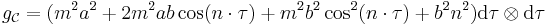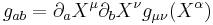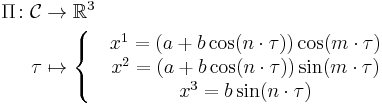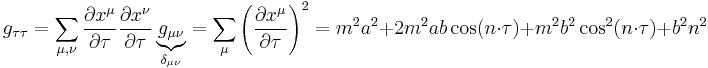Induced metric

In mathematics and theoretical physics, the induced metric is the metric tensor defined on a submanifold which is calculated from the metric tensor on a larger manifold into which the submanifold is embedded. It may be calculated using the following formula:

g_{ab} = \partial_a X^\mu \partial_b X^\nu g_{\mu\nu} (X^\alpha) \

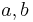Here a,b \ describe the indices of coordinates 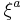\xi^a \ of the submanifold while the functions 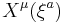X^\mu(\xi^a) \ encode the embedding into the higher-dimensional manifold whose tangent indices are denoted 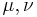\mu,\nu \ . Note: Einstein summation convention was used.

Example - Curve on a torus

Let

\begin{align} \Pi\colon \mathcal{C} &\to \mathbb{R}^3 \\ \tau &\mapsto \left\{\quad\begin{matrix}x^1=(a%2Bb\cos(n\cdot \tau))\cos(m\cdot \tau)\\x^2=(a%2Bb\cos(n\cdot \tau))\sin(m\cdot \tau)\\x^3=b\sin(n\cdot \tau)\end{matrix}\right. \end{align}

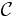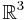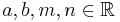be a map from the domain of the curve \mathcal{C} with parameter \tau into the euclidean manifold \mathbb{R}^3. Here a,b,m,n\in\mathbb{R} are constants.

Then there is a metric given on 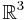\mathbb{R}^3 as

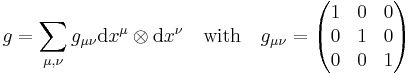g=\sum\limits_{\mu,\nu}g_{\mu\nu}\mathrm{d}x^\mu\otimes \mathrm{d}x^\nu\quad\text{with}\quad g_{\mu\nu} = \begin{pmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{pmatrix} .

and we compute

g_{\tau\tau}=\sum\limits_{\mu,\nu}\frac{\partial x^\mu}{\partial \tau}\frac{\partial x^\nu}{\partial \tau}\underbrace{g_{\mu\nu}}_{\delta_{\mu\nu}} = \sum\limits_\mu\left(\frac{\partial x^\mu}{\partial \tau}\right)^2=m^2 a^2%2B2m^2ab\cos(n\cdot \tau)%2Bm^2b^2\cos^2(n\cdot \tau)%2Bb^2n^2

Therefore g_\mathcal{C}=(m^2 a^2%2B2m^2ab\cos(n\cdot \tau)%2Bm^2b^2\cos^2(n\cdot \tau)%2Bb^2n^2)\mathrm{d}\tau\otimes \mathrm{d}\tau

See also